Methods: Brownian Dynamics Simulations, Multivariate Gaussian analysis, Polymer Physics

While the dynamics of dimers and polymer chains in a viscous solvent is well understood within the celebrated Rouse model, the effect of an external magnetic field on the dynamics of a charged chain is much less understood. We have recently generalised the Rouse model for a charged dimer to include the effect of an external magnetic field. Our analytically solvable model allows a fundamental insight into the magneto-generated dynamics of the dimer in the overdamped limit as induced by the Lorentz-force. Surprisingly, for a dimer of oppositely charged particles, we find an enormous enhancement of the dynamics of the dimer center which exhibits even a transient superballistic behaviour. We attribute this to a significant translation and rotation coupling due to the Lorentz force. How do charged rings behave under magnetic fields? How do the dynamics depend on charge distribution?

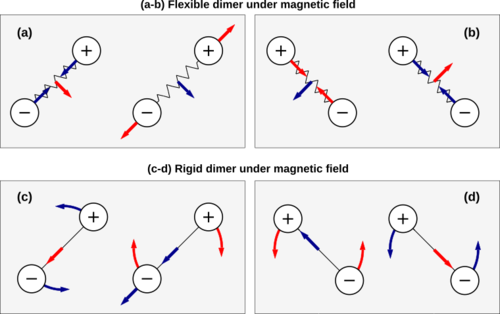
Dimers composed of oppositely charged particles. Blue arrows denote perturbation and the red arrow is its resultant effect. (a,b) In a flexible dimer, movement of the center of mass and bond vector fluctuations are coupled because of the Lorentz force. (a) Bond vector fluctuations move the dimer sideways, which in turn, slows down the spring relaxation. (b) Sideways movement causes the spring to compress. This movement gives rise to Lorentz force that is opposite to the initial direction of applied force. (c-d) Magnetic field couples translation and rotation of a rigid dimer. (c) As the dimer rotates, it gets pushed along its length. This move- ment further gives rise to Lorentz back-torque resulting in a slower rotational diffusion. (d) Translating the dimer along its length causes rotation which then induces Lorentz force opposite to the initial direction of applied force, resulting in reduced mobility along the orientation of the dimer.

The key tasks of the project are listed below. In principle, these can be divided between two bachelor students.

1. Simulate chains and rings of charged particles connected by spring under the effect of an external magnetic field.
2. Determine the dynamics (theoretically) of the Rouse modes. Study the correlation between different modes due to the magnetic field.
3. Calculate the mean first passage time of individual monomers to a specified boundary.

Key words: Rouse model, Lorentz force, Magnetic field

References: